Notebook source code:
notebooks/21_foundations__sub_riemannian_geometry_and_the_heisenberg_group.ipynb
Run it yourself on binder
Tutorial: Sub-Riemannian geometry on the Heisenberg group#
Lead author: Morten Pedersen.
In [1]:
import geomstats.backend as gs
from geomstats.geometry.heisenberg import HeisenbergVectors
from geomstats.geometry.sub_riemannian_metric import SubRiemannianMetric
INFO: Using autograd backend
We import modules for plotting,
In [2]:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # NOQA
The Heisenberg group#
We instantiate the 3D heisenberg group,
In [3]:
heis = HeisenbergVectors(equip=False)
‘heis’ is an object representing a manifold, without any sub-Riemannian structure associated to it.
In geomstats, a sub-Riemannian structure is constructed via the SubRiemannianMetric-class. We now instantiate a SubRiemannianMetric corresponding to the heisenberg group.
In geomstats, a sub-Riemannian metric can be instantiated by supplying either
a function which at an input point outputs the matrix representing the cometric, or
a function which at an input point outputs a matrix whose columns are frame-vectors spanning the distribution at that point. This frame is then implicitly assumed to be orthonormal, so it determines both the distribution and the metric on the tangent bundle.
Defining the Heisenberg sub-Riemannian structure via a frame-field#
We will construct the sub-Riemannian Heisenberg group by supplying a frame-function. Mathematically, we represent the distribution \(\Delta\) in a standard way; at the point \(p \in heis\) the distribution is
where \(F_X = L^{\star}_p(X)\), \(F_Y = L^{\star}_p(Y)\) and \(X = (1,0,0)\), \(Y=(0,1,0)\). So e.g. \(F_X\) is the tangent left translation to point \(p\) of the standard basis vector X in the Lie-algebra. In geomstats, this can be done concisely as follows,
In [4]:
def heis_frame(point):
"""Heiseberg frame."""
translations = heis.jacobian_translation(point)
return translations[..., 0:2]
Given the frame, we now instantiate the sub-Riemannian metric for the Heisenberg group
In [5]:
heis_sr = SubRiemannianMetric(heis, frame=heis_frame)
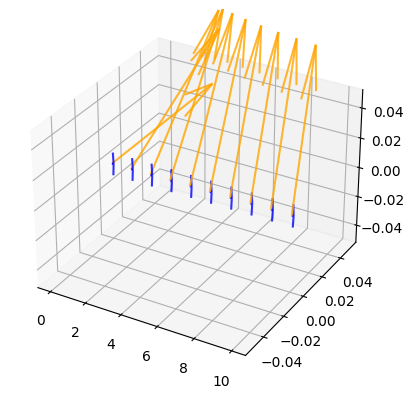
We can illustrate the distribution by plotting the frame-vectors along a line:
In [6]:
line = gs.array([k * gs.array([1.0, 1.0, 1.0]) for k in gs.linspace(0, 10, 10)])
line = gs.array([k * gs.array([1.0, 0.0, 0.0]) for k in gs.linspace(0, 10, 10)])
quiver_length = 0.1
fig1 = plt.figure()
ax = plt.axes(projection="3d")
for i in range(line.shape[0]):
point = line[i, :]
frame_at_point = heis_sr.frame(point)
frame1 = frame_at_point[:, 1]
frame2 = frame_at_point[:, 0]
ax.quiver(
point[0],
point[1],
point[2],
frame1[0],
frame1[1],
frame1[2],
length=quiver_length,
normalize=True,
color="orange",
alpha=0.8,
linestyle="-",
)
ax.quiver(
point[0],
point[1],
point[2],
frame2[0],
frame2[1],
frame2[2],
length=quiver_length,
normalize=True,
color="blue",
alpha=0.8,
linestyle="-",
)
Everything is now set up to generate sub-Riemannian geodesics. A sub-Riemannian geodesic on a manifold \(M\) is determined by an initial point \(p \in M\) and an initial cotangent \(\lambda \in T_p M\).
In [7]:
base_point = gs.array([0.0, 0.0, 0.0])
initial_cotangent = gs.array([1.0, 1.0, 1.0])
times = gs.linspace(0.0, 10.0, 50)
path = heis_sr.geodesic(
initial_point=base_point, initial_cotangent_vec=initial_cotangent, n_steps=1000
)
path_1_1 = path(times)
In [8]:
fig1 = plt.figure()
ax = plt.axes(projection="3d")
ax.scatter(0, 0, 0, marker="+", color="black")
ax.plot3D(
path_1_1[:, 0],
path_1_1[:, 1],
path_1_1[:, 2],
"-",
linewidth=1.5,
markersize=0,
marker=".",
color="green",
alpha=0.7,
)
plt.show()

Sub-Riemannian structures as limits of Riemannian structures#
If the distribution \(\Delta\) is of the same dimension as the manifold at every point, the structure is actually Riemannian. In geomtats, if the manifold is \(n\)-dimensional and we pass a frame function with \(n\) linearly independent vectors at every point, this will generate the Riemannian structure with a metric that makes these vectors orthonormal at every point.
For the heisenberg group, we can use the frame given by left-translation of the standard basis in the Lie algebra,
where \(\epsilon \in [0,1]\). For \(\epsilon=0\) the geodesics will be those of the standard Heisenberg group. For \(\epsilon = 1\) the geodesics will be those of the left-invariant Riemannian metric which on the algebra is simply the euclidean metric.
In [9]:
def heis_frame_riemannian(point, epsilon):
"""Heisenberg Riemannian frame."""
frame_matrix = heis.jacobian_translation(point)
scale_matrix = gs.array([gs.ones((3,)), gs.ones((3,)), gs.ones((3,)) * epsilon]).T
return gs.einsum("...ij,...ij -> ...ij", frame_matrix, scale_matrix)
heis_epsilon_1 = SubRiemannianMetric(
heis, frame=lambda point: heis_frame_riemannian(point, 1)
)
heis_epsilon_0 = SubRiemannianMetric(
heis, frame=lambda point: heis_frame_riemannian(point, 0)
)
In [10]:
base_point = gs.array([0.0, 0.0, 0.0])
initial_cotangent = gs.array([1.0, 1.0, 1.0])
times = gs.linspace(0.0, 10.0, 50)
path_epsilon_1 = heis_epsilon_1.geodesic(
initial_point=base_point, initial_cotangent_vec=initial_cotangent, n_steps=1000
)
path_epsilon_0 = heis_epsilon_0.geodesic(
initial_point=base_point, initial_cotangent_vec=initial_cotangent, n_steps=1000
)
path_1 = path_epsilon_1(times)
path_0 = path_epsilon_0(times)
fig1 = plt.figure()
ax = plt.axes(projection="3d")
ax.scatter(0, 0, 0, marker="+", color="black")
ax.plot3D(
path_1[:, 0],
path_1[:, 1],
path_1[:, 2],
"-",
linewidth=1.5,
markersize=0,
marker=".",
color="green",
alpha=0.7,
label="epsilon = 1",
)
ax.plot3D(
path_0[:, 0],
path_0[:, 1],
path_0[:, 2],
"-",
linewidth=1.5,
markersize=0,
marker=".",
color="red",
alpha=0.7,
label="epsilon = 0",
)
ax.legend()
plt.show()
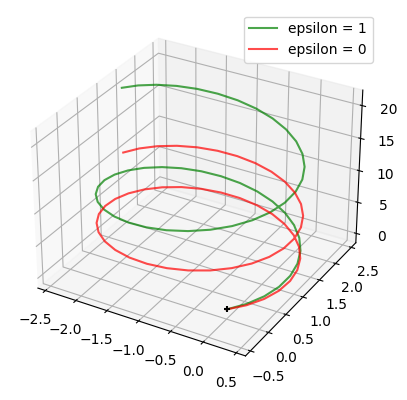
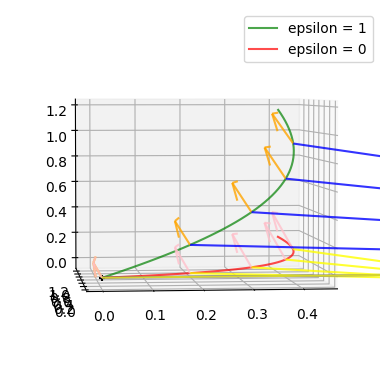
We see that the spiralling structure is similar for the Riemannian (\(\epsilon=1\)) and the sub-Riemannian (\(\epsilon=0\)) geodesics, in fact only their z-coordinates differ. Let’s check that the sub-Riemannian geodesic is horizontal wrt. to the distribution \(\Delta_p = \text{span}(F_X(p), F_Y(p))\) (i.e. it’s tangent vectors lies in \(\Delta\)), whereas the Riemannian one isn’t.
In [11]:
base_point = gs.array([0.0, 0.0, 0.0])
initial_cotangent = gs.array([1.0, 1.0, 1.0])
times = gs.linspace(0.0, 1.0, 50)
path_epsilon_1 = heis_epsilon_1.geodesic(
initial_point=base_point, initial_cotangent_vec=initial_cotangent
)
path_epsilon_0 = heis_epsilon_0.geodesic(
initial_point=base_point, initial_cotangent_vec=initial_cotangent
)
path_1 = path_epsilon_1(times)
path_0 = path_epsilon_0(times)
fig1 = plt.figure()
ax = plt.axes(projection="3d")
ax.scatter(0, 0, 0, marker="+", color="black")
ax.plot3D(
path_1[:, 0],
path_1[:, 1],
path_1[:, 2],
"-",
linewidth=1.5,
markersize=0,
marker=".",
color="green",
alpha=0.7,
label="epsilon = 1",
)
ax.plot3D(
path_0[:, 0],
path_0[:, 1],
path_0[:, 2],
"-",
linewidth=1.5,
markersize=0,
marker=".",
color="red",
alpha=0.7,
label="epsilon = 0",
)
ax.legend()
quiver_length = 1
exp_curve = path_1
for i in range(exp_curve.shape[0]):
if i % 10 == 0:
point = exp_curve[i, :]
frame_at_point = heis_sr.frame(point)
frame1 = frame_at_point[:, 1]
frame2 = frame_at_point[:, 0]
ax.quiver(
point[0],
point[1],
point[2],
frame1[0],
frame1[1],
frame1[2],
length=quiver_length,
normalize=True,
color="orange",
alpha=0.8,
linestyle="-",
)
ax.quiver(
point[0],
point[1],
point[2],
frame2[0],
frame2[1],
frame2[2],
length=quiver_length,
normalize=True,
color="blue",
alpha=0.8,
linestyle="-",
)
quiver_length = 1
exp_curve = path_0
for i in range(exp_curve.shape[0]):
if i % 10 == 0:
point = exp_curve[i, :]
frame_at_point = heis_sr.frame(point)
frame1 = frame_at_point[:, 1]
frame2 = frame_at_point[:, 0]
ax.quiver(
point[0],
point[1],
point[2],
frame1[0],
frame1[1],
frame1[2],
length=quiver_length,
normalize=True,
color="pink",
alpha=0.8,
linestyle="-",
)
ax.quiver(
point[0],
point[1],
point[2],
frame2[0],
frame2[1],
frame2[2],
length=quiver_length,
normalize=True,
color="yellow",
alpha=0.8,
linestyle="-",
)
ax.view_init(3, -96)
plt.show()